狭义相对论是爱因斯坦于1905年在他的一篇论文《论动体的电动力学》提出的，它揭示了时间和空间的关联性。之所以是“电动力学”，可以在后面的讨论中可以看到，狭义相对论的诞生与电磁学的发展是密不可分的。
1 狭义相对论运动学
在同一参考系下，关于物体运动的描述没有变化。物体时空坐标\(\left(\vec{r},t\right)\),速度\(\vec{v}=\frac{d\vec{r}}{dt}\),加速度\(\vec{a}=\frac{d\vec{v}}{dt}=\frac{d^2 \vec{r}}{d t^2}\)。牛顿力学和狭义相对论最大的不同，在于前者时间和空间相互独立，后者则相互关联。因此在不同参考系的时空变换上，两者开始分叉。
在狭义相对论中，最重要的一个观念就是“观测者”，对于同一个事件，在不同坐标系下看到的是不同的结果。对于理解相对论可能产生的一个误区就是，不自觉地把某个事件与一个参考系联系起来，认为其他参考系下的观测是对其的修正，然而事件本身与参考系的选择是相互独立的。
1.1 狭义相对论的基本原理
狭义相对论是建立在两条基本原理之上的：相对性原理和光速不变原理。
光速不变原理：在所有惯性系中，真空光速具有相同量值，与光源的运动无关。
相对性原理：在所有惯性系中，物理学定律具有相同的表达形式。
光速不变原理是基于之前的一系列实验总结出来的。其中有著名的迈克尔逊——莫雷干涉实验，在此实验中光速并未像牛顿力学预知的那样随光源的运动而变化，经典理论出现危机。
关于相对性原理，我学习时则产生了诸多疑惑。牛顿第二定律\(\vec{F}=m\vec{a}\)，在非匀速直线运动参考系中则要加上惯性力修正。因此牛顿假设存在这样一个绝对时空，即一个惯性参考系，牛顿定律在这个参考系下成立，因此惯性参考系是与绝对时空联系在一起，为什么爱因斯坦要特别指明在惯性系中呢？当然，这也是为什么狭义相对论是“狭义”的。爱因斯坦之后听取马赫对惯性系的批判，对其进行修改，这会在广义相对论中进行探讨。
1.2 狭义相对论的坐标变换————洛伦兹变换
在一个参考系中，某一时刻在某一位置发生了一个事件，如何描述它的位置？我们利用时空坐标\(\left(x,y,z,t\right)\)。前三个参数表示它的位置，最后一个参数表示它发生的时刻。我们选定一个空间原点，然后拿一把不变的直尺划定空间标度。同样的，我们选择一个时间零点，然后对整个参考系进行时刻校准，这个过程用的是光，这是光速不变原理的结果。但这不是狭义相对论的主线，不做过多赘述，只需大致理解一下同一个参考系共用一个相同的计时器就行了。
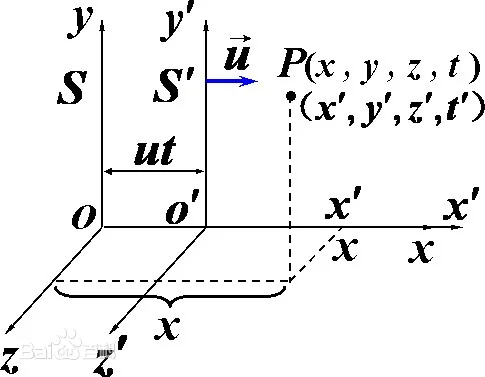先来考虑最简单的情况，对于两个惯性系\(S\),\(S^\prime\),\(S^\prime\)沿\(S\)的\(x\)轴以速度\(\vec{u}\)运动，如图。对于同一个事件，相对于\(S\)静止的观测者观测到它发生在\(\left(x,y,z,t\right)\)，相对于\(S^\prime\)静止的人观测到它发生在\(\left(x^\prime,y^\prime,z^\prime,t^\prime\right)\)，当然这些参数都是相对于各自坐标系的时空原点。
洛伦兹变换就是这两个坐标之间的变换，即两个坐标系之间存在一个映射。我们不妨假定将\(S\)中的时空原点映过去就是\(S^\prime\)中的时空原点，即在各自坐标系的零时刻，两坐标系的空间原点重合。这回简化我们的计算，当然不这么假设也可以，算出来的变换也只是相差一个常数。
那么这个映射是什么呢？首先牛顿第一定律仍然成立，即在\(S\)中加速度为0的物体，在\(S^\prime\)中加速度也为0，则此变换一定是线性的。且坐标轴沿着x轴方向运动，我们可以认为y,z是不变的，则只要讨论x和t的变换。可设： $$x^\prime=a_{11}x+a_{12}t$$ $$t^\prime=a_{21}x+a_{22}t$$ 这个方程有四个未知数，理应有四个方程，这四个方程通过下面这些关系给出。
1.运动相对性：\(S^\prime\)相对于\(S\)向右匀速行驶，从\(S^\prime\)的角度看，\(S\)相对于它向左匀速运动。实际上，如果此时你将两坐标系的x轴翻转一下，这两种运动状态就是一样的（运动坐标系的x轴都指向其运动方向），那么它们都可以适用于上式。此时从\(S^\prime\)的观察者看，坐标\(\left(-x^\prime,t^\prime\right)\)映到坐标\(\left(-x,t\right)\)，满足 $$-x=a_{11}(-x^\prime)+a_{12}t^\prime$$ $$t=a_{21}(-x^\prime)+a_{22}t^\prime$$ 将其带入上一个方程组并化简，得到： $$\left(a_{11}^2-a_{12}a_{21}-1\right)x^\prime+\left(a_{12}a_{22}-a_{11}a_{12}\right)t^\prime=0$$ 由于\(x^\prime\),\(t\)是任意的，则它们的系数等于0，所以： $$ \begin{align} a_{11}^2-a_{12}a_{21}=1\ a_{11}=a_{22}\ \end{align} $$
1.3 狭义相对论的速度变换
由洛伦兹变换可以很快导出速度变换。用\(x^\prime\),\(t^\prime\)的变换式带入\(u^\prime_x=\frac{dx^\prime}{dt^\prime}\)，可求得\(u_x\)的变换式，类似的，可以求得其他几个式子。